This post is a primer on how to test exit poll results with official results using the Hypergeometric distribution function in EXCEL. You can check my computed p-values for the exit poll results using this formula.
The Hypergeometric distribution is used to determine the probability (p-value) of getting a random sample, drawn without replacement, as extreme or more so given the population that the sample is drawn from. If that wording sounds unnecessarily complex, I sympathize. Unfortunately, precision is often complicated to articulate. This definition is hard to parse and you need a working knowledge of what the statistical terms and phrases mean.
“With” versus “without” replacement is an important descriptor of a random sample. A situation with replacement is akin to selecting a card from a deck, then returning it back to the deck before drawing another card. Without replacement is selecting a second card from the 51 remaining in the deck.
This nuance in the drawing of the sample affects the basic assumptions statisticians build equations from. Different statistical distributions have been developed to handle the two situations. Because voters were only asked once to fill out our survey, the exit poll sample is ‘without replacement’ and the Hypergeometric distribution is the most appropriate choice for testing the size of the errors.
Another important and relevant statistical concept: One-sided and Two-sided tests.
Most distributions, including the Hypergeometric distribution, have the majority of data crowded around the average and the data gets sparser the farther away from the average. This type of distribution has ‘tails’. There are the two directions of tails relative to the average value: upper and lower.
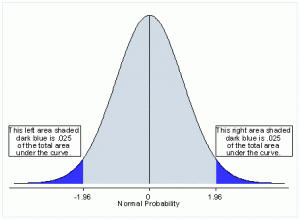
When we perform a statistical test, we are looking at the deviations from what is expected given the underlying distribution of the data. In some cases, we may only be interested in deviations in a particular direction – high or low. In those cases, we can increase the precision of our test by only looking at one end of the distribution. This is called a one-tailed test.
In other situations, we are interested in differences in either direction, so we are examining both the upper and lower tails of the distribution. In our exit polling data, we are looking at the deviations both positive and negative, to determine if either are unusually large. Therefore, it is a two-sided test.
The EXCEL HYPERGEOM.DIST function computes only the lower tail p-value. This result can be manipulated to find the upper tail probability. Both need to be computed. This EXCEL function requires five inputs:
- Sample Success – This is the total number of exit poll surveys for the candidate in that race at that polling place using that voting mechanism.
- Sample size – This is the total number of usable exit poll surveys from voters for that race at that polling place using that voting mechanism.
- Population success – This is the total number of voters for the candidate in that race at that polling place using that voting mechanism.
- Population size – This is the total number of voters for that race at that polling place using that voting mechanism.
- Cumulative – Input 1. This is a technical detail of the statistical test. A zero will result in the probability of getting exactly the results we input, no more and no less. Putting a one here gives the lower tail probability, which is what we want.
EXAMPLE: Hillary Clinton received 435 votes out of 983 cast on the voting machines at the SE site. That’s a 44.25% vote share. Our exit poll data showed Hillary Clinton received 306 votes out of 645 survey responses to this question from voters who cast their votes on those same machines at that polling location. That’s a 47.44% vote share. The difference between those two values, -3.19%, is the error. This error measurement is computed for each candidate, race, type of voting equipment and polling location.
Use EXCEL function HYPERGEOM.DIST with the following inputs:
- Sample_s = 306
- Number_Sample = 645
- Population_s = 435
- Number_pop = 983
- Cumulative = 1
Lower Tail P-value for Clinton, Machine Votes, SE Wichita
= HYPERGEOM.DIST(306,645,435,983,1) = 0.9979
Whoa!! I thought you said Hillary got cheated? This result is a near certainty.
That’s because our exit poll sample had a larger percentage of Hillary voters than the official results did. Her exit poll results lie in the upper tail of the distribution, well above the official average. We just computed the p-value for the lower tail i.e. the probability of randomly getting as many Hillary votes as we did (306) or LESS.
Next we need to compute the probability of randomly getting as many exit poll votes as she did or MORE. The upper tail of the distribution. Through the magic of math, we can find the upper tail probability with a modification to this function.
Subtract 1 from our sample size and compute the lower tail probability for that sample size. Then subtract that lower tail probability from 1 to get the correct upper tail p-value.
Upper Tail p-value for Clinton, Machine Votes, SE Wichita
= 1.0 – HYPERGEOM.DIST(305,645,435,983,1) = .00325
Finally, because we did not specify in advance what direction we expected to see, this is a two-tailed test. For two-tailed tests of this nature, the p-value is computed as double the minimum one-tailed p-value, capped at 1.0.
Two-tailed p-value for Clinton, Machine Votes, SE Wichita = 2*0.00325 = 0.0065.
Finally, putting it all together in one cell, nesting the needed functions:
Two-tailed p-value for Clinton, Machine Votes, SE Wichita
=2*MIN(+HYPGEOM.DIST(306,645,435,983,1), 1-HYPGEOM.DIST(305,645,435,983,1), 0.5)
Picture from http://www.ats.ucla.edu/stat/mult_pkg/faq/pvalue1.gif